Difference between revisions of "Grid Connection - Wind Energy"
***** (***** | *****) |
***** (***** | *****) m |
||
| Line 1: | Line 1: | ||
| − | |||
| − | + | == Overview - Grid Configuration<br/> == | |
| − | + | <u>For analyzing the grid impact of a wind farm connection at (exemplary)<ref>Content of this page from: GTZ 2009: Grid Integration of Wind Energy in the Western Cape. p. 7 http://www.gtz.de/de/dokumente/gtz2009-en-grid-study-western-cape.pdf</ref> 120kV, the following main aspects have to be studied:</u> | |
| + | *Impact on thermal limits in the surrounding subtransmssion network<br/> | ||
| + | *Impact on voltage variations at the connection point and the surrounding subtransmssion system:<br/> | ||
| + | *Impact on short circuit levels<br/> | ||
| + | *Impact on Power Quality aspects (Harmonics/Flicker, IEC 61400-21)<br/> | ||
| − | + | <br/>Each of these aspects requires different types of studies and modelling approaches.<br/> | |
| − | <br | + | <br/> |
| − | + | == Impact on Thermal Limits in the Surrounding Subtransmission Network<br/> == | |
| − | |||
| − | |||
| − | |||
| − | + | In a first step, it is required to verify that the existing network capacity is able to take the additionally generated power. For this purpose, credible contingencies, such as n-1 branch outages, have to be analyzed.<br/>An n-1 analysis based on load flow calculations of all surrounding lines leads to the conclusion that there is a thermal overload problem in the case that one circuit between (in the example that follows) Laingsburg and Boskloof is on outage and the wind farm production is above 120MW. For all other contingencies, no thermal problems can be identified.<br/> | |
| − | * | + | <br/>The worst case situation with a wind farm production of 150MW and the outage of one of the parallel circuits is depicted in Figure 1. As shown in this diagram, the circuit that will remain in service will carry a load of 127% of its thermal rating.<br/><u>The general options for mitigating such problems are:</u><br/> |
| − | * | + | *Reinforce the existing line or build a new line. |
| + | *[[Grid Connection - Wind Energy#Probabilistic Assessment of the Non Delivered Energy in the Case of Wind Farm Limitation|Limit the wind farm]] during all times. | ||
| + | *[[Grid Connection - Wind Energy#Limit the Wind Farm Output in the Case of an Actual Line Failure|Limit wind farm output in case of actual line failure]] (manual or automatic inter-trip). | ||
| + | *Consider [[Grid Connection - Wind Energy#Dynamic Line Rating Systems|dynamic line rating]] systems.<br/> | ||
| − | + | <br/> | |
| − | < | + | Generally, the most economic solution under the constraint that a secure network operation is ensured should be taken. <u>However, the costs associated with each of the four options depend on:</u><br/> |
| + | *Length of the line | ||
| + | *Number of hours per year during which the overload situation occurs (and during which the wind farm output would have to be limited)<br/> | ||
| − | <br> | + | <br/> |
| − | + | For this reason, only a probabilistic assessment considering the actual wind speed conditions at the site can provide an answer to the question, which mitigation option should finally be applied.<br/> | |
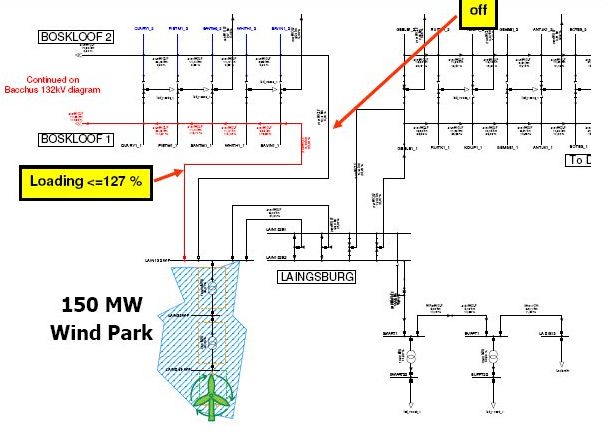
| − | + | <br/>[[File:Outage wind park example.JPG|frame|center|180px|Figure 1: Outage of one of the parallel 132kV lines between Laingsburg and Boskloof]] <ref>id. pp.8</ref><br/> | |
| − | *Equivalent power curve of the wind farm | + | <br/> |
| + | |||
| + | === Probabilistic Assessment of the Non Delivered Energy in the Case of Wind Farm Limitation<br/> === | ||
| + | |||
| + | For analyzing the second [[Grid Connection - Wind Energy#Impact on Thermal Limits in the Surrounding Subtransmission Network|mitigation option]]; that is, limiting the wind farm output to 120 MW during all times (80 % of rated output), the probability that the actually generated power exceeds a level of 80% of installed capacity has to be assessed. <u>For this assessment, the following information is required in addition to a load flow model of the zone of interest:</u><br/> | ||
| + | *Equivalent power curve of the wind farm | ||
*Average wind speed and, if available, the Weibull-shape factor of the wind speed distribution. | *Average wind speed and, if available, the Weibull-shape factor of the wind speed distribution. | ||
| − | In the case that no more detailed information is available, which is usually the case in an early planning stage; a typical power curve of a wind generator can be used as equivalent wind farm power curve. Effects, like wind-farm internal losses etc. can be considered in the equivalent wind farm power curve. <br>Based on average wind speed and shape factor, the distribution of wind-speeds can be calculated, based on a Weibull distribution. Together with the equivalent wind farm power curve, a wind generation duration curve for one wind farm can be calculated showing the probability for the case that the generated wind power exceeds a given level (see Figure 3).<br>The energy that cannot be delivered to the system can then be evaluated by calculating the area between that part of the red curve that is above the blue line indicating the wind farm limit and the blue line itself. For a monetary analysis, this area has to be multiplied by the assumed tariff.<br> | + | In the case that no more detailed information is available, which is usually the case in an early planning stage; a typical power curve of a wind generator can be used as equivalent wind farm power curve. Effects, like wind-farm internal losses etc. can be considered in the equivalent wind farm power curve.<br/>Based on average wind speed and shape factor, the distribution of wind-speeds can be calculated, based on a Weibull distribution. Together with the equivalent wind farm power curve, a wind generation duration curve for one wind farm can be calculated showing the probability for the case that the generated wind power exceeds a given level (see Figure 3).<br/>The energy that cannot be delivered to the system can then be evaluated by calculating the area between that part of the red curve that is above the blue line indicating the wind farm limit and the blue line itself. For a monetary analysis, this area has to be multiplied by the assumed tariff.<br/> |
| + | |||
| + | <br/> | ||
| + | |||
| + | '''The example of Laingsburg (Western Cape, South Africa):'''<br/> | ||
| − | + | In case of the wind farm at Laingsburg, there were no wind speed data available. For this reason, the corresponding assessment has been carried out for an assumed average wind speed of 7 m/s and 8 m/s. this assessment will provide a good idea about the order of magnitude of the monetary losses associated with a wind farm limitation and at the same time show the sensitivity of this value against average wind speed.<br/>Capping a single wind farm with 7m/s average wind speed at 80% results in a not delivered energy of approximately 5% of the totally available energy. This would be equivalent to around 19 000 MWh/year, which could not be delivered. Assuming a tariff of 1,25 Rand/kWh, the resulting economic losses to the wind farm operators would be in the order of magnitude of 23 750 000 R/year.<br/>If instead 8m/s average wind speed is assumed an considering also an 80% power output limit, the results indicate a not delivered energy of approximately 7,5% of the totally available energy. This would be equivalent to around 37 000 MWh/year, which could not be delivered, resulting in 46 250 000 R/year of losses.<br/> | |
| − | + | [[File:Wind speed example.JPG|frame|center|180px|Figure 2: Wind speed distribution and power duration curve for an average wind speed of 7m/s]] | |
| − | + | <ref>id. p. 11</ref><br/> | |
| − | + | <br/> | |
| − | < | + | === Limit the Wind Farm Output in the Case of an Actual Line Failure<br/> === |
| − | <br> | + | Alternatively, if network operation guidelines allow so, it would be much more economical to limit the wind farm output only under situations, in which one of the circuits between Laingsburg and Boskloof is actually out of service, e.g. because of a planned or an unplanned outage.<br/>In cases, in which there is only a minor overload on the remaining circuit, like in the situation here, it would be possible to limit the wind farm output by a manual post-fault action executed by the network operator.<br/>Alternatively, or in situations in which there is a major overload (above the emergency rating of the line) it is advisable to install an automatic intertrip-schemes that trips some of the wind turbines in the wind farm in the case that the circuit breakers of one of the two parallel circuits are opened.<br/> |
| − | + | <br/> | |
| − | + | === Dynamic Line Rating Systems<br/> === | |
| − | + | <u>The rating of overhead lines depends on:</u><br/> | |
| + | *Ambient temperature | ||
| + | *Wind speed and wind direction<br/> | ||
| − | + | <br/> | |
| − | + | In case of cool weather and/or under high wind speeds, overhead lines experience a much better cooling and hence have a much higher rating than under high temperature and/or low wind speed conditions.<br/>Because of the positive correlation between line rating and wind farm output, the installation of a dynamic line rating system at the critical double circuit line can be a very useful option for avoiding grid congestions.<br/> | |
| − | |||
| − | + | <br/><u>Dynamic line rating systems are either based on:</u><br/> | |
| + | *Measurement of the conductor temperature | ||
| + | *Measurement of the line sag | ||
| + | *Measurement of ambient conditions<br/> | ||
| − | + | <br/> | |
| − | |||
| − | |||
| − | or combinations of some of the above listed measurements. Together with a thermal model of the line, it is possible to predict the actual rating of the line at any moment in time.<br> | + | or combinations of some of the above listed measurements. Together with a thermal model of the line, it is possible to predict the actual rating of the line at any moment in time.<br/> |
| − | + | <br/> | |
| − | + | == Impact on Voltage Variations at the Connection Point and the Surrounding Subtransmission Network<br/> == | |
| − | *Identifying the required var-control mode (voltage/droop/const. power factor) | + | Besides the impact on thermal limits, load flow and contingency analysis studies allow analyzing the impact of wind generation on voltage variations during normal operations and during contingencies.<br/>In a wind generation impact study, the required level of reactive power support of wind farms need to be identified in an early planning stage. <u>Therefore, studies are typically carried out aiming at:</u><br/> |
| − | *Identifying the required reactive power range | + | *Identifying the required var-control mode (voltage/droop/const. power factor) |
| − | *Identifying the need of additional reactive compensation devices in the system. | + | *Identifying the required reactive power range |
| + | *Identifying the need of additional reactive compensation devices in the system.<br/> | ||
| − | + | <br/> | |
| − | + | === Reactive Power Control Modes<br/> === | |
| − | + | The least cost effective solution for a wind farm is the operation at constant power factor close to unity of each individual WTG, for which no park-controller is required. This is the classical approach for small wind farms (only a few turbines) connected to distribution grids (<=33kV).<br/> | |
| − | <br> | + | In case of wind farms connected to subtransmssion or transmission levels, the system operators usually asks the wind farm operator to maintain a constant power factor, a constant reactive power setting or even the voltage at the grid connection point.<br/>Hardware costs of the WTGs depend on the required power factor range (or reactive power range) of each individual WTG. In case of wind farms connected to a transmission or subtransmission level, the power factor range required at the grid connection point is not equal to the power factor range of each WTG because the reactive power need of the step-up transformers and the main grid-transformer has to be covered by the WTGs too. For this reason, there is usually additional shunt capacitors connected near to the grid connection point for complying with reactive power requirements of the system operator.<br/>When requiring the operation with unity power factory at the grid connection point, the power factor range of typical WTGs is usually sufficient for covering the reactive power demand of wind farm internal components.<br/>When asking for a wider power factor range at the grid connection point, e.g. 0,95, WTGs with wider reactive power range and/or additional shunt capacitors are usually required.<br/>Voltage control requires a feed-back loop of the voltage and continuously varying reactive adjustment of the WTGs. Depending on the dynamic requirements (speed of operation) and the required reactive power range of the WTGs, it will be possible to realize voltage control by WTGs and additional shunt capacitors or even additional dynamic reactive power compensation devices, such as SVC or STATCOM might be required, which can have a very high cost impact.<br/>Droop control refers to a combined voltage-reactive power control defined by a v-Q characteristic, according to which reactive power is adjusted. Droop control is typically used for fast acting reactive power compensation devices, such as STATCOMs or SVCs.<br/> |
| − | + | <br/> | |
| − | + | === Impact Studies<br/> === | |
| − | *Varying wind speed (varying active power generation) | + | The purpose of system impact studies should be to identify the required reactive power control mode, the required reactive power range and dynamic performance requirements. It is important to consider cost aspects, as described in the previous section for avoiding unnecessary investments.<br/>The feasibility of a wind farm consisting of wind generators that operate with constant power factor (at MV-side of WTG step-up transformers) can be evaluated by analyzing P-V-curves for normal operating conditions and for a set of critical contingencies.<br/><u>P-V curves can be used for analyzing voltage variations resulting from:</u><br/> |
| + | *Varying wind speed (varying active power generation) | ||
*Contingencies | *Contingencies | ||
| − | The P-V curves depicted in Figure 4 apply to normal operating conditions (red curve) and three contingencies (line outages) in the neighborhood of the planned wind farm for the operation with a constant power factor of cos(phi)=1 at the MV-side of each WTG step-up transformer.<br> | + | The P-V curves depicted in Figure 4 apply to normal operating conditions (red curve) and three contingencies (line outages) in the neighborhood of the planned wind farm for the operation with a constant power factor of cos(phi)=1 at the MV-side of each WTG step-up transformer.<br/> |
| − | <br> | + | <br/> |
| − | According to the results shown in Figure 4, the maximum voltage at the wind farm connection point would exceed the usual +5% limit and the voltage variation against active power variations would be in the range of approximately 5%. Hence operation with unity power factory would lead to unacceptable voltage variations.<br>It can further be observed from Figure 4 that voltage step changes because of line outages in the neighborhood of the wind farm are within very reasonable limits (around 1%) and don’t cause any problem.<br>The typical approach for mitigating voltage problems, which are due to varying active power levels, is to operate the wind farm with an active power dependent power factor (absorbing vars). This is a very cost effective solution because such a reactive power or power factor characteristic can easily be implemented inside the controller of each individual WTG and doesn’t require any voltage feed-back or global wind farm controller.<br>The resulting PV-curve is depicted in Figure 5. These curves are based on a wind farm with a minimum power factor of 0,95 (absorbing) at the wind farm connection point. The voltage now stays within the required voltage band and voltage variations against active power variations stay within acceptable limits of less than 2%. <br> | + | According to the results shown in Figure 4, the maximum voltage at the wind farm connection point would exceed the usual +5% limit and the voltage variation against active power variations would be in the range of approximately 5%. Hence operation with unity power factory would lead to unacceptable voltage variations.<br/>It can further be observed from Figure 4 that voltage step changes because of line outages in the neighborhood of the wind farm are within very reasonable limits (around 1%) and don’t cause any problem.<br/>The typical approach for mitigating voltage problems, which are due to varying active power levels, is to operate the wind farm with an active power dependent power factor (absorbing vars). This is a very cost effective solution because such a reactive power or power factor characteristic can easily be implemented inside the controller of each individual WTG and doesn’t require any voltage feed-back or global wind farm controller.<br/>The resulting PV-curve is depicted in Figure 5. These curves are based on a wind farm with a minimum power factor of 0,95 (absorbing) at the wind farm connection point. The voltage now stays within the required voltage band and voltage variations against active power variations stay within acceptable limits of less than 2%.<br/> |
| − | <br> | + | <br/> |
| − | [[ | + | [[File:PV curves for wind-Farm.JPG|frame|center|180px|Figure 3: PV curves for wind farm operation with unity power factor at the connection point]] |
| − | <br> | + | <br/> |
| − | [[ | + | [[File:PV curves for wind-Farm coshi.JPG|frame|center|180px|Figure 4: PV curves considering a cosphi(P)Characteristic]] <ref>id. p. 18</ref><br/> |
| − | <br> | + | <br/> |
| − | == Impact on Short Circuit Currents<br> | + | == Impact on Short Circuit Currents<br/> == |
| − | In the case of a grid impact study, the main purpose of short circuit studies is to verify that the short circuit rating of existing equipment such as bus bars, circuit breakers, lines or cables remains within the required limits.<br>Additionally, short circuit studies are required for verifying the settings of line or transformer protection relays in the network.<br> | + | In the case of a grid impact study, the main purpose of short circuit studies is to verify that the short circuit rating of existing equipment such as bus bars, circuit breakers, lines or cables remains within the required limits.<br/>Additionally, short circuit studies are required for verifying the settings of line or transformer protection relays in the network.<br/> |
| − | <br> | + | <br/> |
| − | === Special Modeling Considerations<br> | + | === Special Modeling Considerations<br/> === |
| − | <br> [[ | + | <br/>[[File:Short circuit currents.JPG|frame|center|180px|Figure 5: Short circuits currents of a DFIG (HV-side of step-up transformer)]]<br/><ref>id. p. 16</ref><br/> |
| − | Modern, variable speed wind generators, which are either based on doubly-fed induction generators or generators with fully rated converter, are difficult to model for standard, steady state short circuit analysis (e.g IEC 60909 or ANSI C37) because of the following reasons:<br> | + | <u>Modern, variable speed wind generators, which are either based on doubly-fed induction generators or generators with fully rated converter, are difficult to model for standard, steady state short circuit analysis (e.g IEC 60909 or ANSI C37) because of the following reasons:</u><br/> |
| + | *If in the time frame of a few milliseconds only, these turbines are influenced by their controllers, making their behavior nonlinear, even during these short time periods. | ||
| + | *Doubly-fed induction generators are usually equipped with special protection mechanisms (e.g. crow bar, Chopper-resistance) that trigger during voltage dips.<br/> | ||
| − | + | <br/> | |
| − | |||
| − | The curves depicted in Figure 6 show the currents of a doubly-fed induction generator in case of a short circuit.<br>The generator of this example is equipped with a crow-bar for protecting the rotor-side converter against high currents and high DC-voltages.<br> | + | The curves depicted in Figure 6 show the currents of a doubly-fed induction generator in case of a short circuit.<br/>The generator of this example is equipped with a crow-bar for protecting the rotor-side converter against high currents and high DC-voltages.<br/> |
| − | During the period, in which the crow-bar is inserted (first 50ms after fault insertion), AC-components of the short circuit currents are very low because of the field-damping effect of the crow-bar. After the crow-bar has been removed, the converter controllers support the voltage by increasing reactive currents. Therefore, AC components of the short circuit current are again increasing but stay in the range of normal operating currents.<br>This means that doubly-fed induction machine wind generators have a considerable contribution to peak short circuit currents.<br>In the longer term however, when the controllers have taken over again, fault currents will be in a range of normal operating currents, depending on the reactive current control concept of the turbines. Because there are many Grid Codes around the world that require the injection of reactive currents during situations of low voltages and because voltage support usually helps the turbines to ride through low voltage conditions, many wind generators inject reactive currents during situations of low voltages and thereby contribute to AC-components of short circuit currents.<br> | + | During the period, in which the crow-bar is inserted (first 50ms after fault insertion), AC-components of the short circuit currents are very low because of the field-damping effect of the crow-bar. After the crow-bar has been removed, the converter controllers support the voltage by increasing reactive currents. Therefore, AC components of the short circuit current are again increasing but stay in the range of normal operating currents.<br/>This means that doubly-fed induction machine wind generators have a considerable contribution to peak short circuit currents.<br/>In the longer term however, when the controllers have taken over again, fault currents will be in a range of normal operating currents, depending on the reactive current control concept of the turbines. Because there are many Grid Codes around the world that require the injection of reactive currents during situations of low voltages and because voltage support usually helps the turbines to ride through low voltage conditions, many wind generators inject reactive currents during situations of low voltages and thereby contribute to AC-components of short circuit currents.<br/> |
| − | <br>'''Equivalent Synchronous Machine Model'''<br>Because of the mentioned difficulties with the modeling of variable speed wind generators for steady state short circuit analysis, simplified modeling approaches are required for the inclusion of variable speed wind generators in IEC 60909 or ANSI C37-type short circuit calculations.<br | + | <br/>'''Equivalent Synchronous Machine Model'''<br/>Because of the mentioned difficulties with the modeling of variable speed wind generators for steady state short circuit analysis, simplified modeling approaches are required for the inclusion of variable speed wind generators in IEC 60909 or ANSI C37-type short circuit calculations.<br/> |
| − | *The subtransient reactance is typically defined in a way, that the WTG contribution to peak short circuit currents is reflected correctly. | + | <br/><u>The typical approach, which is used in many places around the world is nowadays based on an “equivalent synchronous machine” modeling approach, in which variable speed wind generators are approximated by an equivalent circuit with subtransient and transient reactance:</u><br/> |
| − | *The equivalent transient reactance typically defines the machine’s behavior during situations, in which the controllers have taken over again. | + | *The subtransient reactance is typically defined in a way, that the WTG contribution to peak short circuit currents is reflected correctly. |
| + | *The equivalent transient reactance typically defines the machine’s behavior during situations, in which the controllers have taken over again.<br/> | ||
| − | + | <br/> | |
| − | <br> | + | Unfortunately, this approach is not able to provide very accurate results for the short circuit contribution of wind farms. It should only be used for planning studies, when the short circuit rating of existing substations, lines and transformers has to be verified.<br/>In the case that accurate short circuit currents have to be calculated, e.g. for analyzing malfunctioning of protection relays, time domain simulations based on accurate dynamic WTG models are required.<br/> |
| − | < | + | <br/>[[File:Model aggregation.JPG|frame|center|180px|Figure 6: Aggregated Wind Farm Model for System Impact Studies]]<br/> |
| − | <br> | + | <ref>id. pp. 13</ref><br/> |
| − | + | <br/> | |
| + | In case of grid impact studies, where the impact of a new wind farm on short circuit ratings of existing equipment is analyzed, an aggregated wind farm model can be used. Typically, wind farms are modeled by one equivalent generator and one equivalent step-up transformer having n times the size of each individual WTG and step-up transformer (see Figure 7).<br/>The impedance of wind farm internal cables can be neglected if maximum short circuit currents are in the centre of interest of the studies.<br/><u>We can therefore summarize the following:</u><br/> | ||
*Double Fed Induction Generator (DFIG): | *Double Fed Induction Generator (DFIG): | ||
| − | - Considerable contribution to peak short circuit current.<br>- Contribution to thermal short circuit ratings: approx 1 p.u. shc-current<br> | + | - Considerable contribution to peak short circuit current.<br/>- Contribution to thermal short circuit ratings: approx 1 p.u. shc-current<br/> |
| − | |||
*WTG with fully rated converter: | *WTG with fully rated converter: | ||
| − | - Contribution to initial short circuit current: approx. 1 p.u. shc-current<br | + | - Contribution to initial short circuit current: approx. 1 p.u. shc-current<br/> |
| − | |||
| − | |||
| − | *Contribution to initial shc-current (Ikss): approx 2 kA (at 132kV) | + | - Contribution to thermal short circuit ratings: approx 1 p.u. shc-current<br/>In the case of a 150MW wind farm at Laingsburg this results in the following short circuit contribution from the wind farm:<br/> |
| − | *Contribution to peak shc-current (ip): 4,4 kA | + | *Contribution to initial shc-current (Ikss): approx 2 kA (at 132kV) |
| + | *Contribution to peak shc-current (ip): 4,4 kA | ||
*Contribution to transient shc-current (Iks): 0,67 kA | *Contribution to transient shc-current (Iks): 0,67 kA | ||
| − | The short circuit contribution of the wind farm is not critical in this particular example because the fault level at the wind farm connection point is very low and the substation is operated far below its short circuit rating.<br | + | The short circuit contribution of the wind farm is not critical in this particular example because the fault level at the wind farm connection point is very low and the substation is operated far below its short circuit rating.<br/> |
| − | |||
| − | |||
| − | + | <br/> | |
| − | == | + | == Impact on Harmonics<br/> == |
| − | Harmonic | + | === Harmonic Current Injection Studies of Wind Farms<br/> === |
| − | *Low order harmonics are typically resulting from grid commutated converters or saturation effects. Their phase angle is therefore grid synchronized resulting in high correlation of the injected harmonic currents. | + | Harmonic current injection studies are typically carried out based on wind turbine measurement report according to IEC 61400-21, which lists the worst-case harmonic current injection at each harmonic frequency at which a current injection >0,1% of rated current can be observed.<br/>'''Superposition'''<br/>Because it is very much unlikely, the all wind generators in a wind farm inject worst case harmonic currents with the same phase angle at the same time, assumptions for the diversity with which harmonic currents are injected into the grid by the different wind generators can be made.<br/>The generally applied international standard that defines rules for these assumptions is IEC 61000-3-6. <u>The basic consideration of these rules is that:</u><br/> |
| + | *Low order harmonics are typically resulting from grid commutated converters or saturation effects. Their phase angle is therefore grid synchronized resulting in high correlation of the injected harmonic currents. | ||
*High order harmonics are typically resulting from self commutated power electronics converters. Their phase angel is therefore highly uncorrelated. | *High order harmonics are typically resulting from self commutated power electronics converters. Their phase angel is therefore highly uncorrelated. | ||
| − | |||
| − | |||
| − | + | For considering these effects, IEC 61000-3-6 defines formulas allowing calculating the superposition of harmonic voltage distortions resulting from harmonic current injection of different harmonic sources.<br/>For wind generation, Summation Law 2 according to IEC 61000-3-6 is typically applied.<br/>Summation Law 2 is based on the following formula for each harmonic order h and each harmonic source i:<br/>[[File:Formula harmonic order h harmonic source i.JPG|frame|center|180px|Formula: harmonic order h harmonic source i]] <ref>id. p. 19</ref> | |
| − | |||
| − | |||
| − | + | <u>with:</u><br/> | |
| + | *a=1 for h<=4 | ||
| + | *a=1.4 for h<5 and h<=13 | ||
| + | *a=2 for h>13 | ||
| − | + | The practical application of this formula requires the calculation of the harmonic voltage distortion at the connection point caused by each harmonic source (wind generator) in the system and calculating the resulting harmonic voltage distortion by evaluating the formula above.<br/> | |
| − | <br>''' | + | <br/>'''Wind Farms with Short Connection to the Grid'''<br/>For wind farms that are directly connected to the grid with a step-up transformer and without any considerable HV-AC cables, a simplified version of this formula can be applied, as proposed in IEC 61400-21. According to IEC61400-21, the harmonic current injections of the entire wind farm can be modelled by one equivalent harmonic current source at the grid connection point. The harmonic current injection at every harmonic frequency is calculated using (1) and by replacing voltage by current.<br/>In these cases, harmonic voltage distortion can simply by calculated by taking the harmonic impedance at the grid connection point with the highest magnitude and multiplying it with resulting harmonic current. 2.8.1.3 Wind Farms with Long Cable Connection to the Grid Wind farms that are connected to the grid via considerable HV-AC cable (e.g. offshore wind farms) require more sophisticated harmonic analysis because there is always a high risk for harmonic resonance problems because of the cable capacitance. The actual location of resonance frequencies may vary with the operating conditions of the transmission grid. Therefore, harmonic voltage distortion must be calculated for the full range of harmonic impedances at the PCC, as it has been worked out by the system operator and by applying (1) for considering the impact of all wind generators in the wind farm on harmonic voltage distortions.<br/>The worst case harmonic voltage distortion is then reported and the basis of filter sizing, if a filter will be required.<br/> |
| − | <br>''' | + | <br/>'''Special Modelling Considerations'''<br/>In some turbine designs, local filters are used, which can have a considerable impact, especially in the case of low order cable resonance problems in the system.<br/>Measurement reports according to IEC 61400-21 only report magnitude of harmonic currents measured at the LV-side. A worst case assumption consists of assuming that the entire harmonic contents appear either in positive or negative sequence system. In case of 3rd, 6th, 9th, etc. harmonics, this definitely represents a worst case assumption because the largest part of third order harmonic currents typically appears in the zero sequence. In the case that the studies show problems at these frequencies, this should be further analyzed, e.g. by looking at harmonic currents measured at the HV-side of the wind turbine step-up transformers (MV-level).<br/> |
| − | <br> | + | <br/>'''In-the-Field Measurements'''<br/>It is common practice to install a power quality meter in the grid connection point that monitors harmonic voltages at the PCC and harmonic currents injected by the wind farm during wind farm operation.<br/> |
| − | + | <br/> | |
| − | == | + | == Impact on Flicker<br/> == |
| − | + | === General Methodology<br/> === | |
| − | *Continuous active power variations of the wind generators, e.g. resulting from wind turbulence. | + | <u>Flicker, being a variation of the fundamental frequency voltage, can be a result of:</u><br/> |
| + | *Continuous active power variations of the wind generators, e.g. resulting from wind turbulence. | ||
*Switching actions within in the wind farm. | *Switching actions within in the wind farm. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | for the relevant impedance angle at the grid connection point must be taken from a wind turbine measurement sheet according to IEC 61400-21.<br>These values together with the minimum fault level at the grid connection point allow calculating:<br> | + | Flicker assessment for wind farms is typically carried out according to IEC 61000-3-7 and IEC 61400-21. The method requires the calculation of the minimum short circuit level and impedance angle at the PCC.<br/><u>Based on the impedance angle, the maximum values for:</u><br/> |
| + | *Flicker coefficient c | ||
| + | *Flicker step-factor kf | ||
| + | *Flicker step-factor ku | ||
| + | *Max. number of switching operations N10 | ||
| + | *Max. number of switching operations N120<br/> | ||
| + | |||
| + | |||
| + | |||
| + | for the relevant impedance angle at the grid connection point must be taken from a wind turbine measurement sheet according to IEC 61400-21.<br/><u>These values together with the minimum fault level at the grid connection point allow calculating:</u><br/> | ||
| + | *Short-term and long term flicker value (Pst/Plt) during continuous operation. | ||
| + | *Short-term and long term flicker value (Pst/Plt) due to switching actions | ||
| + | |||
| + | for one wind generator.<br/>For assessing the Flicker of an entire wind farm, IEC 61400-21 states that it can be assumed that the flicker relevant components of wind turbulence and other flicker-relevant aspects are uncorrelated within the wind farm.<br/>For this reason, the following formula can be applied for calculating the flicker of an entire wind farm with n turbines based on the flicker of one individual WTG:<br/>[[File:Formula flicker.JPG|frame|center|153px|Formula: Flicker of individual WTG]]<ref>id. p. 22</ref><br/>With Psti being the short-term flicker of one individual WTG. This means in other words, that the total flicker of a wind farm with n WTGs is lower by a factor of 1/ n than the flicker that would be caused by an individual WTG with n times the size.<br/> | ||
| + | |||
| + | |||
| + | |||
| + | == Technical Requirements<br/> == | ||
| + | |||
| + | <u>With regard to particular technical requirements of wind generators, the following general recommendations can be made:</u><br/> | ||
| + | *Frequency and voltage range of operation should be defined analogously to the existing practice in a country; | ||
| + | *A reactive power range at the grid connection point of (+/- 0,33 p.u./Prated, cos(phi)>0,95) under full load and partial load conditions will be sufficient. It is recommended to decide on a case-by-case basis, whether reactive power control capability during low and no wind hours will be required. | ||
| + | *For wind farms that will be connected to subtransmission and distribution levels, operation with constant power factory will be sufficient. If required, an active power dependent [[Grid Connection - Wind Energy#Reactive Power Control Modes|reactive power characteristic should]] be foreseen. | ||
| + | *Wind farms that will be connected to the main transmission level should have the technical capability for controlling the reactive power or the voltage (feed-back voltage control) at the grid connection point. The required dynamic performance of such voltage control has to be identified with the help of additional, dynamic studies. | ||
| + | *Because of the overall amount of planned wind generation in the Cape, all wind generators should be equipped with '''fault ride-through (FRT)''' capability for avoiding WTG trips in case of line faults. | ||
| + | |||
| − | |||
| − | |||
| − | + | For standardizing the technical characteristics of wind generators in a country, it is recommended to extend the national grid code by Connection Conditions for wind generation. These Connection Conditions should consider existing standards with respect to the connection of thermal and hydro power plants and make provision of the particular technical characteristics of wind generators.<br/> | |
| − | |||
| − | |||
| − | + | = Further Information = | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[https://energypedia.info/Portal:Wind Portal:Wind]<br/> | |
| − | |||
| − | |||
| − | + | == References == | |
| − | <br> | + | <references /><br/> |
[[Category:Wind]] | [[Category:Wind]] | ||
| + | [[Category:Grid]] | ||
| + | [[Category:South_Africa]] | ||
Revision as of 12:38, 24 July 2013
Overview - Grid Configuration
For analyzing the grid impact of a wind farm connection at (exemplary)[1] 120kV, the following main aspects have to be studied:
- Impact on thermal limits in the surrounding subtransmssion network
- Impact on voltage variations at the connection point and the surrounding subtransmssion system:
- Impact on short circuit levels
- Impact on Power Quality aspects (Harmonics/Flicker, IEC 61400-21)
Each of these aspects requires different types of studies and modelling approaches.
Impact on Thermal Limits in the Surrounding Subtransmission Network
In a first step, it is required to verify that the existing network capacity is able to take the additionally generated power. For this purpose, credible contingencies, such as n-1 branch outages, have to be analyzed.
An n-1 analysis based on load flow calculations of all surrounding lines leads to the conclusion that there is a thermal overload problem in the case that one circuit between (in the example that follows) Laingsburg and Boskloof is on outage and the wind farm production is above 120MW. For all other contingencies, no thermal problems can be identified.
The worst case situation with a wind farm production of 150MW and the outage of one of the parallel circuits is depicted in Figure 1. As shown in this diagram, the circuit that will remain in service will carry a load of 127% of its thermal rating.
The general options for mitigating such problems are:
- Reinforce the existing line or build a new line.
- Limit the wind farm during all times.
- Limit wind farm output in case of actual line failure (manual or automatic inter-trip).
- Consider dynamic line rating systems.
Generally, the most economic solution under the constraint that a secure network operation is ensured should be taken. However, the costs associated with each of the four options depend on:
- Length of the line
- Number of hours per year during which the overload situation occurs (and during which the wind farm output would have to be limited)
For this reason, only a probabilistic assessment considering the actual wind speed conditions at the site can provide an answer to the question, which mitigation option should finally be applied.
Probabilistic Assessment of the Non Delivered Energy in the Case of Wind Farm Limitation
For analyzing the second mitigation option; that is, limiting the wind farm output to 120 MW during all times (80 % of rated output), the probability that the actually generated power exceeds a level of 80% of installed capacity has to be assessed. For this assessment, the following information is required in addition to a load flow model of the zone of interest:
- Equivalent power curve of the wind farm
- Average wind speed and, if available, the Weibull-shape factor of the wind speed distribution.
In the case that no more detailed information is available, which is usually the case in an early planning stage; a typical power curve of a wind generator can be used as equivalent wind farm power curve. Effects, like wind-farm internal losses etc. can be considered in the equivalent wind farm power curve.
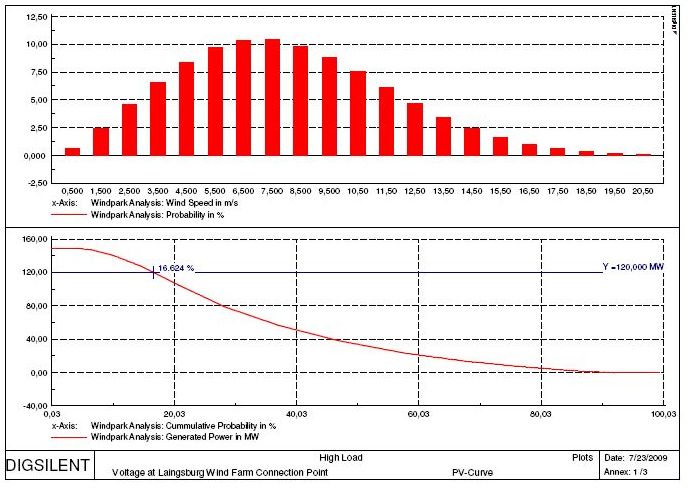
Based on average wind speed and shape factor, the distribution of wind-speeds can be calculated, based on a Weibull distribution. Together with the equivalent wind farm power curve, a wind generation duration curve for one wind farm can be calculated showing the probability for the case that the generated wind power exceeds a given level (see Figure 3).
The energy that cannot be delivered to the system can then be evaluated by calculating the area between that part of the red curve that is above the blue line indicating the wind farm limit and the blue line itself. For a monetary analysis, this area has to be multiplied by the assumed tariff.
The example of Laingsburg (Western Cape, South Africa):
In case of the wind farm at Laingsburg, there were no wind speed data available. For this reason, the corresponding assessment has been carried out for an assumed average wind speed of 7 m/s and 8 m/s. this assessment will provide a good idea about the order of magnitude of the monetary losses associated with a wind farm limitation and at the same time show the sensitivity of this value against average wind speed.
Capping a single wind farm with 7m/s average wind speed at 80% results in a not delivered energy of approximately 5% of the totally available energy. This would be equivalent to around 19 000 MWh/year, which could not be delivered. Assuming a tariff of 1,25 Rand/kWh, the resulting economic losses to the wind farm operators would be in the order of magnitude of 23 750 000 R/year.
If instead 8m/s average wind speed is assumed an considering also an 80% power output limit, the results indicate a not delivered energy of approximately 7,5% of the totally available energy. This would be equivalent to around 37 000 MWh/year, which could not be delivered, resulting in 46 250 000 R/year of losses.
Limit the Wind Farm Output in the Case of an Actual Line Failure
Alternatively, if network operation guidelines allow so, it would be much more economical to limit the wind farm output only under situations, in which one of the circuits between Laingsburg and Boskloof is actually out of service, e.g. because of a planned or an unplanned outage.
In cases, in which there is only a minor overload on the remaining circuit, like in the situation here, it would be possible to limit the wind farm output by a manual post-fault action executed by the network operator.
Alternatively, or in situations in which there is a major overload (above the emergency rating of the line) it is advisable to install an automatic intertrip-schemes that trips some of the wind turbines in the wind farm in the case that the circuit breakers of one of the two parallel circuits are opened.
Dynamic Line Rating Systems
The rating of overhead lines depends on:
- Ambient temperature
- Wind speed and wind direction
In case of cool weather and/or under high wind speeds, overhead lines experience a much better cooling and hence have a much higher rating than under high temperature and/or low wind speed conditions.
Because of the positive correlation between line rating and wind farm output, the installation of a dynamic line rating system at the critical double circuit line can be a very useful option for avoiding grid congestions.
Dynamic line rating systems are either based on:
- Measurement of the conductor temperature
- Measurement of the line sag
- Measurement of ambient conditions
or combinations of some of the above listed measurements. Together with a thermal model of the line, it is possible to predict the actual rating of the line at any moment in time.
Impact on Voltage Variations at the Connection Point and the Surrounding Subtransmission Network
Besides the impact on thermal limits, load flow and contingency analysis studies allow analyzing the impact of wind generation on voltage variations during normal operations and during contingencies.
In a wind generation impact study, the required level of reactive power support of wind farms need to be identified in an early planning stage. Therefore, studies are typically carried out aiming at:
- Identifying the required var-control mode (voltage/droop/const. power factor)
- Identifying the required reactive power range
- Identifying the need of additional reactive compensation devices in the system.
Reactive Power Control Modes
The least cost effective solution for a wind farm is the operation at constant power factor close to unity of each individual WTG, for which no park-controller is required. This is the classical approach for small wind farms (only a few turbines) connected to distribution grids (<=33kV).
In case of wind farms connected to subtransmssion or transmission levels, the system operators usually asks the wind farm operator to maintain a constant power factor, a constant reactive power setting or even the voltage at the grid connection point.
Hardware costs of the WTGs depend on the required power factor range (or reactive power range) of each individual WTG. In case of wind farms connected to a transmission or subtransmission level, the power factor range required at the grid connection point is not equal to the power factor range of each WTG because the reactive power need of the step-up transformers and the main grid-transformer has to be covered by the WTGs too. For this reason, there is usually additional shunt capacitors connected near to the grid connection point for complying with reactive power requirements of the system operator.
When requiring the operation with unity power factory at the grid connection point, the power factor range of typical WTGs is usually sufficient for covering the reactive power demand of wind farm internal components.
When asking for a wider power factor range at the grid connection point, e.g. 0,95, WTGs with wider reactive power range and/or additional shunt capacitors are usually required.
Voltage control requires a feed-back loop of the voltage and continuously varying reactive adjustment of the WTGs. Depending on the dynamic requirements (speed of operation) and the required reactive power range of the WTGs, it will be possible to realize voltage control by WTGs and additional shunt capacitors or even additional dynamic reactive power compensation devices, such as SVC or STATCOM might be required, which can have a very high cost impact.
Droop control refers to a combined voltage-reactive power control defined by a v-Q characteristic, according to which reactive power is adjusted. Droop control is typically used for fast acting reactive power compensation devices, such as STATCOMs or SVCs.
Impact Studies
The purpose of system impact studies should be to identify the required reactive power control mode, the required reactive power range and dynamic performance requirements. It is important to consider cost aspects, as described in the previous section for avoiding unnecessary investments.
The feasibility of a wind farm consisting of wind generators that operate with constant power factor (at MV-side of WTG step-up transformers) can be evaluated by analyzing P-V-curves for normal operating conditions and for a set of critical contingencies.
P-V curves can be used for analyzing voltage variations resulting from:
- Varying wind speed (varying active power generation)
- Contingencies
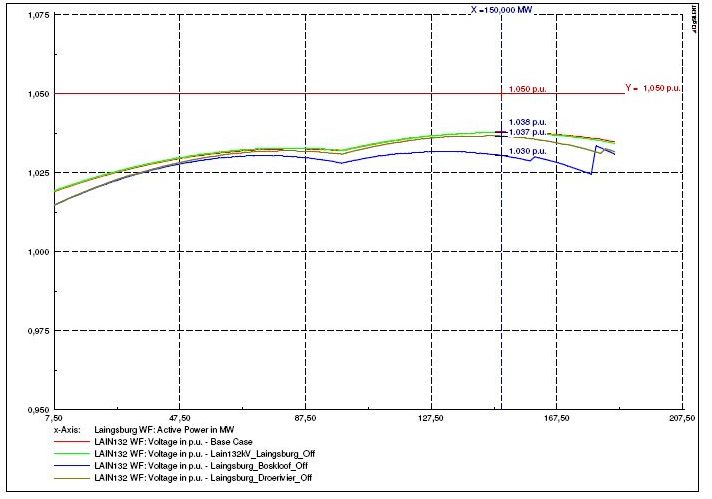
The P-V curves depicted in Figure 4 apply to normal operating conditions (red curve) and three contingencies (line outages) in the neighborhood of the planned wind farm for the operation with a constant power factor of cos(phi)=1 at the MV-side of each WTG step-up transformer.
According to the results shown in Figure 4, the maximum voltage at the wind farm connection point would exceed the usual +5% limit and the voltage variation against active power variations would be in the range of approximately 5%. Hence operation with unity power factory would lead to unacceptable voltage variations.
It can further be observed from Figure 4 that voltage step changes because of line outages in the neighborhood of the wind farm are within very reasonable limits (around 1%) and don’t cause any problem.
The typical approach for mitigating voltage problems, which are due to varying active power levels, is to operate the wind farm with an active power dependent power factor (absorbing vars). This is a very cost effective solution because such a reactive power or power factor characteristic can easily be implemented inside the controller of each individual WTG and doesn’t require any voltage feed-back or global wind farm controller.
The resulting PV-curve is depicted in Figure 5. These curves are based on a wind farm with a minimum power factor of 0,95 (absorbing) at the wind farm connection point. The voltage now stays within the required voltage band and voltage variations against active power variations stay within acceptable limits of less than 2%.
Impact on Short Circuit Currents
In the case of a grid impact study, the main purpose of short circuit studies is to verify that the short circuit rating of existing equipment such as bus bars, circuit breakers, lines or cables remains within the required limits.
Additionally, short circuit studies are required for verifying the settings of line or transformer protection relays in the network.
Special Modeling Considerations
Modern, variable speed wind generators, which are either based on doubly-fed induction generators or generators with fully rated converter, are difficult to model for standard, steady state short circuit analysis (e.g IEC 60909 or ANSI C37) because of the following reasons:
- If in the time frame of a few milliseconds only, these turbines are influenced by their controllers, making their behavior nonlinear, even during these short time periods.
- Doubly-fed induction generators are usually equipped with special protection mechanisms (e.g. crow bar, Chopper-resistance) that trigger during voltage dips.
The curves depicted in Figure 6 show the currents of a doubly-fed induction generator in case of a short circuit.
The generator of this example is equipped with a crow-bar for protecting the rotor-side converter against high currents and high DC-voltages.
During the period, in which the crow-bar is inserted (first 50ms after fault insertion), AC-components of the short circuit currents are very low because of the field-damping effect of the crow-bar. After the crow-bar has been removed, the converter controllers support the voltage by increasing reactive currents. Therefore, AC components of the short circuit current are again increasing but stay in the range of normal operating currents.
This means that doubly-fed induction machine wind generators have a considerable contribution to peak short circuit currents.
In the longer term however, when the controllers have taken over again, fault currents will be in a range of normal operating currents, depending on the reactive current control concept of the turbines. Because there are many Grid Codes around the world that require the injection of reactive currents during situations of low voltages and because voltage support usually helps the turbines to ride through low voltage conditions, many wind generators inject reactive currents during situations of low voltages and thereby contribute to AC-components of short circuit currents.
Equivalent Synchronous Machine Model
Because of the mentioned difficulties with the modeling of variable speed wind generators for steady state short circuit analysis, simplified modeling approaches are required for the inclusion of variable speed wind generators in IEC 60909 or ANSI C37-type short circuit calculations.
The typical approach, which is used in many places around the world is nowadays based on an “equivalent synchronous machine” modeling approach, in which variable speed wind generators are approximated by an equivalent circuit with subtransient and transient reactance:
- The subtransient reactance is typically defined in a way, that the WTG contribution to peak short circuit currents is reflected correctly.
- The equivalent transient reactance typically defines the machine’s behavior during situations, in which the controllers have taken over again.
Unfortunately, this approach is not able to provide very accurate results for the short circuit contribution of wind farms. It should only be used for planning studies, when the short circuit rating of existing substations, lines and transformers has to be verified.
In the case that accurate short circuit currents have to be calculated, e.g. for analyzing malfunctioning of protection relays, time domain simulations based on accurate dynamic WTG models are required.
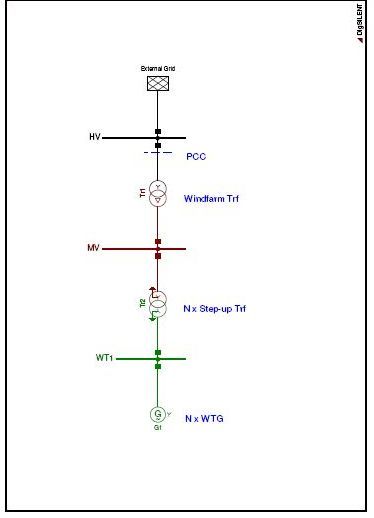
In case of grid impact studies, where the impact of a new wind farm on short circuit ratings of existing equipment is analyzed, an aggregated wind farm model can be used. Typically, wind farms are modeled by one equivalent generator and one equivalent step-up transformer having n times the size of each individual WTG and step-up transformer (see Figure 7).
The impedance of wind farm internal cables can be neglected if maximum short circuit currents are in the centre of interest of the studies.
We can therefore summarize the following:
- Double Fed Induction Generator (DFIG):
- Considerable contribution to peak short circuit current.
- Contribution to thermal short circuit ratings: approx 1 p.u. shc-current
- WTG with fully rated converter:
- Contribution to initial short circuit current: approx. 1 p.u. shc-current
- Contribution to thermal short circuit ratings: approx 1 p.u. shc-current
In the case of a 150MW wind farm at Laingsburg this results in the following short circuit contribution from the wind farm:
- Contribution to initial shc-current (Ikss): approx 2 kA (at 132kV)
- Contribution to peak shc-current (ip): 4,4 kA
- Contribution to transient shc-current (Iks): 0,67 kA
The short circuit contribution of the wind farm is not critical in this particular example because the fault level at the wind farm connection point is very low and the substation is operated far below its short circuit rating.
Impact on Harmonics
Harmonic Current Injection Studies of Wind Farms
Harmonic current injection studies are typically carried out based on wind turbine measurement report according to IEC 61400-21, which lists the worst-case harmonic current injection at each harmonic frequency at which a current injection >0,1% of rated current can be observed.
Superposition
Because it is very much unlikely, the all wind generators in a wind farm inject worst case harmonic currents with the same phase angle at the same time, assumptions for the diversity with which harmonic currents are injected into the grid by the different wind generators can be made.
The generally applied international standard that defines rules for these assumptions is IEC 61000-3-6. The basic consideration of these rules is that:
- Low order harmonics are typically resulting from grid commutated converters or saturation effects. Their phase angle is therefore grid synchronized resulting in high correlation of the injected harmonic currents.
- High order harmonics are typically resulting from self commutated power electronics converters. Their phase angel is therefore highly uncorrelated.
For considering these effects, IEC 61000-3-6 defines formulas allowing calculating the superposition of harmonic voltage distortions resulting from harmonic current injection of different harmonic sources.
For wind generation, Summation Law 2 according to IEC 61000-3-6 is typically applied.
Summation Law 2 is based on the following formula for each harmonic order h and each harmonic source i:
with:
- a=1 for h<=4
- a=1.4 for h<5 and h<=13
- a=2 for h>13
The practical application of this formula requires the calculation of the harmonic voltage distortion at the connection point caused by each harmonic source (wind generator) in the system and calculating the resulting harmonic voltage distortion by evaluating the formula above.
Wind Farms with Short Connection to the Grid
For wind farms that are directly connected to the grid with a step-up transformer and without any considerable HV-AC cables, a simplified version of this formula can be applied, as proposed in IEC 61400-21. According to IEC61400-21, the harmonic current injections of the entire wind farm can be modelled by one equivalent harmonic current source at the grid connection point. The harmonic current injection at every harmonic frequency is calculated using (1) and by replacing voltage by current.
In these cases, harmonic voltage distortion can simply by calculated by taking the harmonic impedance at the grid connection point with the highest magnitude and multiplying it with resulting harmonic current. 2.8.1.3 Wind Farms with Long Cable Connection to the Grid Wind farms that are connected to the grid via considerable HV-AC cable (e.g. offshore wind farms) require more sophisticated harmonic analysis because there is always a high risk for harmonic resonance problems because of the cable capacitance. The actual location of resonance frequencies may vary with the operating conditions of the transmission grid. Therefore, harmonic voltage distortion must be calculated for the full range of harmonic impedances at the PCC, as it has been worked out by the system operator and by applying (1) for considering the impact of all wind generators in the wind farm on harmonic voltage distortions.
The worst case harmonic voltage distortion is then reported and the basis of filter sizing, if a filter will be required.
Special Modelling Considerations
In some turbine designs, local filters are used, which can have a considerable impact, especially in the case of low order cable resonance problems in the system.
Measurement reports according to IEC 61400-21 only report magnitude of harmonic currents measured at the LV-side. A worst case assumption consists of assuming that the entire harmonic contents appear either in positive or negative sequence system. In case of 3rd, 6th, 9th, etc. harmonics, this definitely represents a worst case assumption because the largest part of third order harmonic currents typically appears in the zero sequence. In the case that the studies show problems at these frequencies, this should be further analyzed, e.g. by looking at harmonic currents measured at the HV-side of the wind turbine step-up transformers (MV-level).
In-the-Field Measurements
It is common practice to install a power quality meter in the grid connection point that monitors harmonic voltages at the PCC and harmonic currents injected by the wind farm during wind farm operation.
Impact on Flicker
General Methodology
Flicker, being a variation of the fundamental frequency voltage, can be a result of:
- Continuous active power variations of the wind generators, e.g. resulting from wind turbulence.
- Switching actions within in the wind farm.
Flicker assessment for wind farms is typically carried out according to IEC 61000-3-7 and IEC 61400-21. The method requires the calculation of the minimum short circuit level and impedance angle at the PCC.
Based on the impedance angle, the maximum values for:
- Flicker coefficient c
- Flicker step-factor kf
- Flicker step-factor ku
- Max. number of switching operations N10
- Max. number of switching operations N120
for the relevant impedance angle at the grid connection point must be taken from a wind turbine measurement sheet according to IEC 61400-21.
These values together with the minimum fault level at the grid connection point allow calculating:
- Short-term and long term flicker value (Pst/Plt) during continuous operation.
- Short-term and long term flicker value (Pst/Plt) due to switching actions
for one wind generator.
For assessing the Flicker of an entire wind farm, IEC 61400-21 states that it can be assumed that the flicker relevant components of wind turbulence and other flicker-relevant aspects are uncorrelated within the wind farm.
For this reason, the following formula can be applied for calculating the flicker of an entire wind farm with n turbines based on the flicker of one individual WTG:
[8]
With Psti being the short-term flicker of one individual WTG. This means in other words, that the total flicker of a wind farm with n WTGs is lower by a factor of 1/ n than the flicker that would be caused by an individual WTG with n times the size.
Technical Requirements
With regard to particular technical requirements of wind generators, the following general recommendations can be made:
- Frequency and voltage range of operation should be defined analogously to the existing practice in a country;
- A reactive power range at the grid connection point of (+/- 0,33 p.u./Prated, cos(phi)>0,95) under full load and partial load conditions will be sufficient. It is recommended to decide on a case-by-case basis, whether reactive power control capability during low and no wind hours will be required.
- For wind farms that will be connected to subtransmission and distribution levels, operation with constant power factory will be sufficient. If required, an active power dependent reactive power characteristic should be foreseen.
- Wind farms that will be connected to the main transmission level should have the technical capability for controlling the reactive power or the voltage (feed-back voltage control) at the grid connection point. The required dynamic performance of such voltage control has to be identified with the help of additional, dynamic studies.
- Because of the overall amount of planned wind generation in the Cape, all wind generators should be equipped with fault ride-through (FRT) capability for avoiding WTG trips in case of line faults.
For standardizing the technical characteristics of wind generators in a country, it is recommended to extend the national grid code by Connection Conditions for wind generation. These Connection Conditions should consider existing standards with respect to the connection of thermal and hydro power plants and make provision of the particular technical characteristics of wind generators.
Further Information